傅立叶变换原理动画图（通俗易懂的傅里叶变换）

在数据处理过程中经常会用到傅里叶变换把时域谱变成频域谱。因为是操作软件，即使不懂，也能获得正确结果。

傅里叶变换对于多数人来讲，怎么学都学不会，弄不懂，最后干脆就放弃了。实际上，圈外人只想知道其一不想知道其二即可。抱有这样想法的人可以看一看本文，这是我看到的最通俗易懂的解释，未必严谨，保你有个初级感性认知。

傅立叶变换的使用途径之一是对声波数据进行傅立叶变换，就能知道声音中包含多少高音和低音。

人在发声的时候，喉部的声带是振动的。声带的振动使空气震动，形成波(声波)，声波通过空气到达鼓膜，从而产生声音。所谓声音的高低，是由该声波每秒的振动次数决定的。振动的次数越多，声音就越高，反之，振动的次数越少，声音就越低，请看下图。

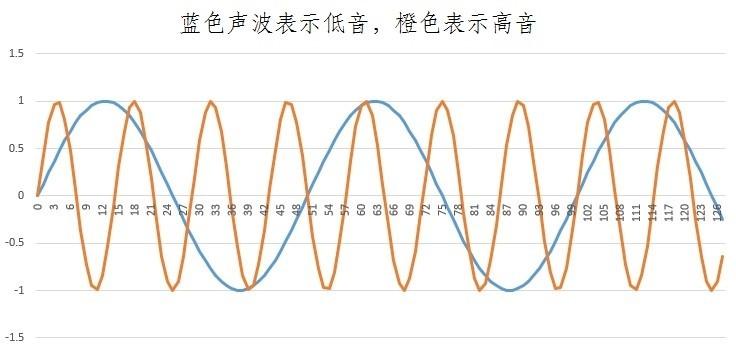
比起蓝色的波形，橙色的波形有更多的波峰和波谷。如果把这一波形看作声波的话，橙声波比蓝声波振动的次数多，所以橙声波的声音更高。对声波使用傅里叶变换的话，就能知道声波的振动情况。接下来我们用傅立叶变换来实际调查声波的振动次数。

先对蓝色声波进行傅立叶变换，看看振动的样子。

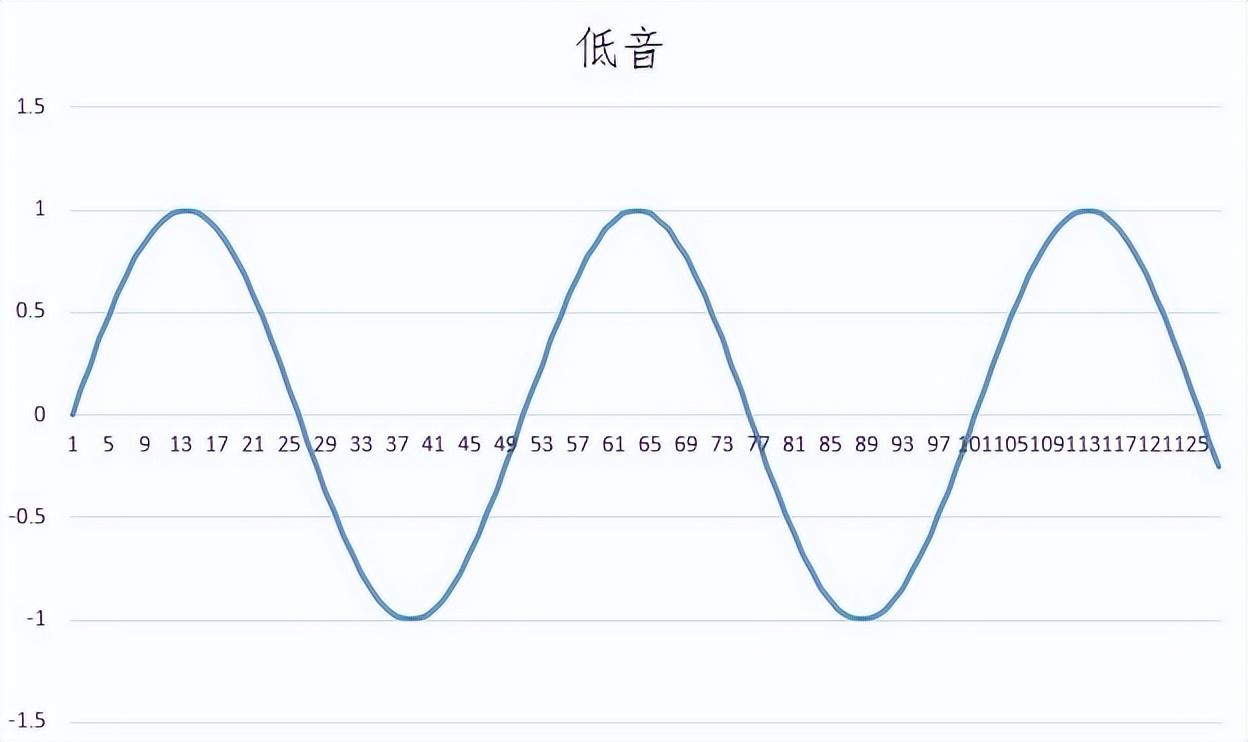
为了让大家更容易理解，下面展示的一些傅立叶变换后的波形，实际上是在傅立叶变换后做了一些修改的。

下面的图片是对蓝色声波进行傅立叶变换后的波形。

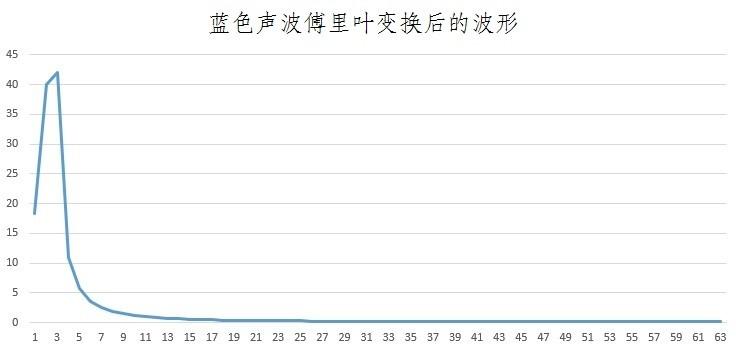
在观察傅立叶变换后的波形时，出现的波峰横轴位置非常重要。上图中的波峰横轴位于2到3的正中间，约为2.5的位置。这个2.5表示的是将波形的波谷作为一组来计算时的组数。让我们再确认一下刚才的波形。

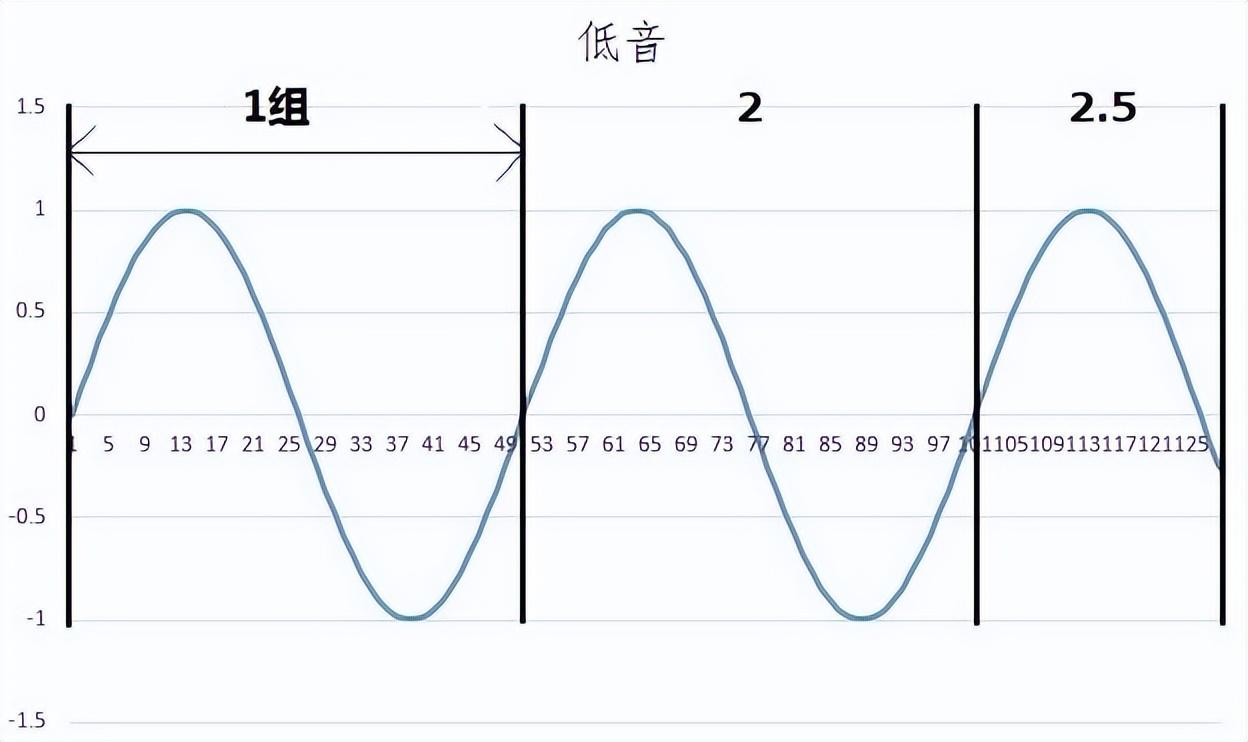
如果把波峰和波谷作为一组来计算的话，可以看出总共约有2.5组。最后的部分没有波谷，只有波峰，所以为1组的一半，0.5组。

在刚才傅立叶变换的波形中，2.5附近出现了波峰，与蓝色声波的组数一致。

接下来对橙色声波进行傅立叶变换。

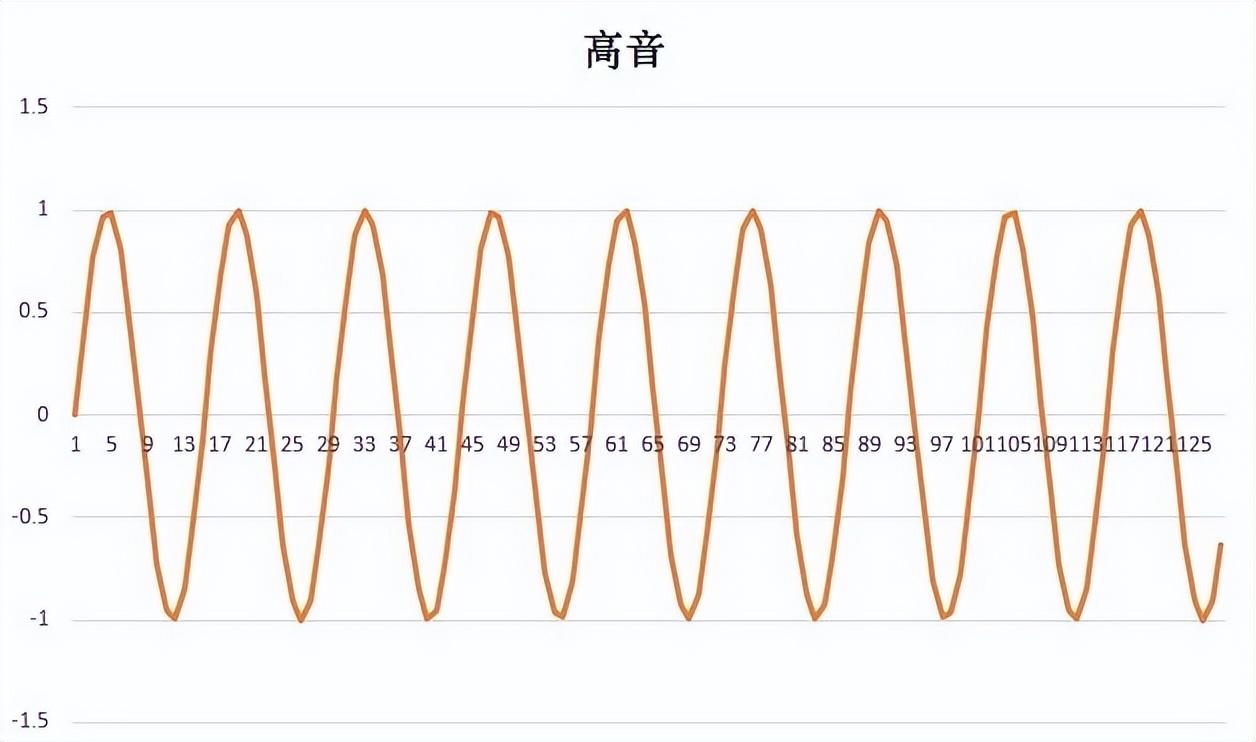
结果就变成了下面的波形。

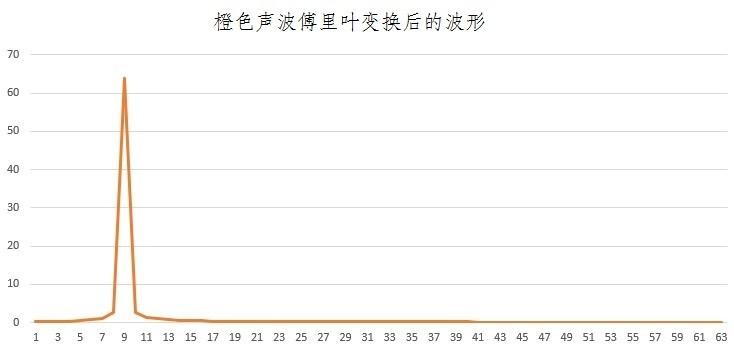
横轴为9的地方有一个波峰。一边看着橙色的波形，一边数着波峰和波谷的组数，最后的组数约为9组。

在橙色波形中，傅立叶变换的结果和从波形中读取的组数一致。像这样进行傅立叶变换，就可以知道波峰和波谷的数量(也就是振动的次数)。

但是，如果只是这样的话，可能会有人说:想知道波峰和波谷的组数的话，不用傅立叶变换，看着波形数不就行了吗？实际上，发挥傅立叶变换威力时候才刚刚开始。现在，让我们数一数下面复杂的波形图像中的组数。

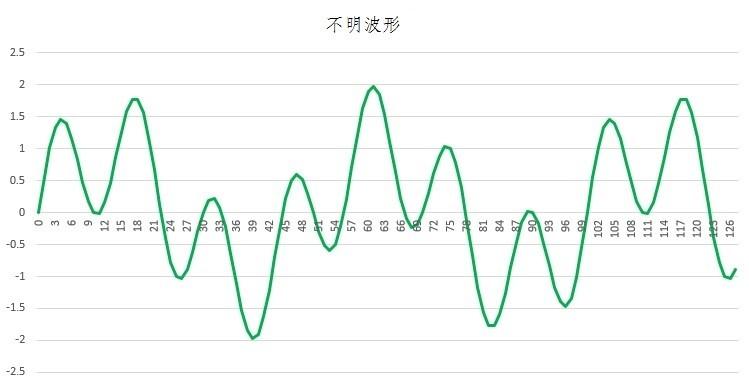
即使想数组数，也不知道从哪里到哪里算一组比较好。那么，让我们对这个波形进行傅里叶变换吧。于是出现了这样的波形。

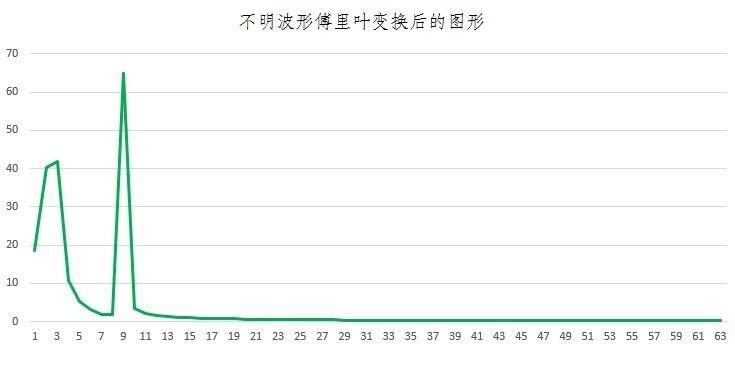
横轴为2.5和9的附近各有一个波峰。大家注意到了吗？2.5是指蓝色声波的波谷数，9是指橙色声波的波谷数。

其实，刚才复杂的绿波是由蓝波和橙波相加而成的。

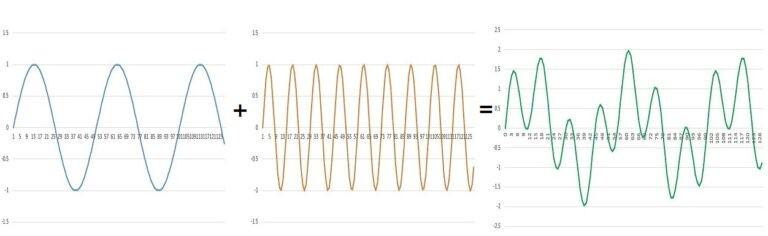
像这样复杂的波实际上是由几个简单的波组合而成的。通过傅立叶变换，可以从复杂的波中分离出隐藏的简单波。